La prédiction des prix des actions est un défi complexe et captivant qui attire l’attention des investisseurs, des analystes financiers et des chercheurs depuis des décennies. Dans le contexte actuel du marché financier, Tesla, Inc. émerge comme une entreprise emblématique, non seulement en raison de son impact sur l’industrie automobile, mais également en raison de son rôle central dans le secteur en rapide évolution des véhicules électriques. La période allant du 1er janvier 2013 au 11 octobre 2023 a été particulièrement remarquable pour Tesla, marquée par des avancées technologiques, des lancements de produits novateurs et une volatilité significative de ses actions en bourse. Tesla, Inc. a émergé comme un acteur majeur dans l’industrie automobile, stimulant un intérêt particulier pour la prévision de ses prix d’actions. Cette étude se concentre sur la période allant du 1er janvier 2013 au 11 octobre 2023, explorant la pertinence des machines à vecteurs de support (SVM) en tant que modèle prédictif pour le cours des actions de Tesla. Les SVM, en tant qu’algorithmes d’apprentissage automatique, présentent une capacité unique à traiter des relations non linéaires entre les données, ce qui les rend appropriés pour modéliser la complexité des marchés financiers. En intégrant des données historiques, économiques et sectorielles, cette étude vise à évaluer l’efficacité des SVM dans la prédiction des prix des actions de Tesla sur la période spécifiée. L’objectif est d’apporter des perspectives nouvelles sur la manière dont ces modèles peuvent être exploités pour anticiper les fluctuations du marché, en mettant en lumière les schémas et les tendances qui ont marqué l’évolution des actions de Tesla au fil des années.

Support Vector Machine (SVM)

Les machines à vecteurs de support (SVM), également connues sous le nom de Support Vector Machines en anglais, constituent un algorithme populaire utilisé pour résoudre de nombreux problèmes de classification et de régression. Elles font partie des modèles d’apprentissage supervisé basés sur le concept d’hyperplans en tant que frontières de décision. Dans un espace bidimensionnel, l’hyperplan se présente sous la forme d’une ligne. La machine à vecteurs de support (SVM) est une extension du classifieur de machine à vecteurs de support qui résulte de l’agrandissement de l’espace des caractéristiques d’une manière spécifique, en utilisant une technique appelée noyau. Les trois noyaux fondamentaux des machines à vecteurs de support (SVM) apportent des approches distinctes pour la modélisation de relations complexes dans les données. Le noyau linéaire, simple et efficace, crée des frontières de décision linéaires, tandis que le noyau polynomial et le noyau RBF élargissent cette capacité en permettant la représentation de relations non linéaires à travers des transformations polynomiales et gaussiennes, respectivement. Chacun de ces noyaux offre des avantages spécifiques, permettant aux SVM de s’adapter à une variété de scénarios de classification et de régression.

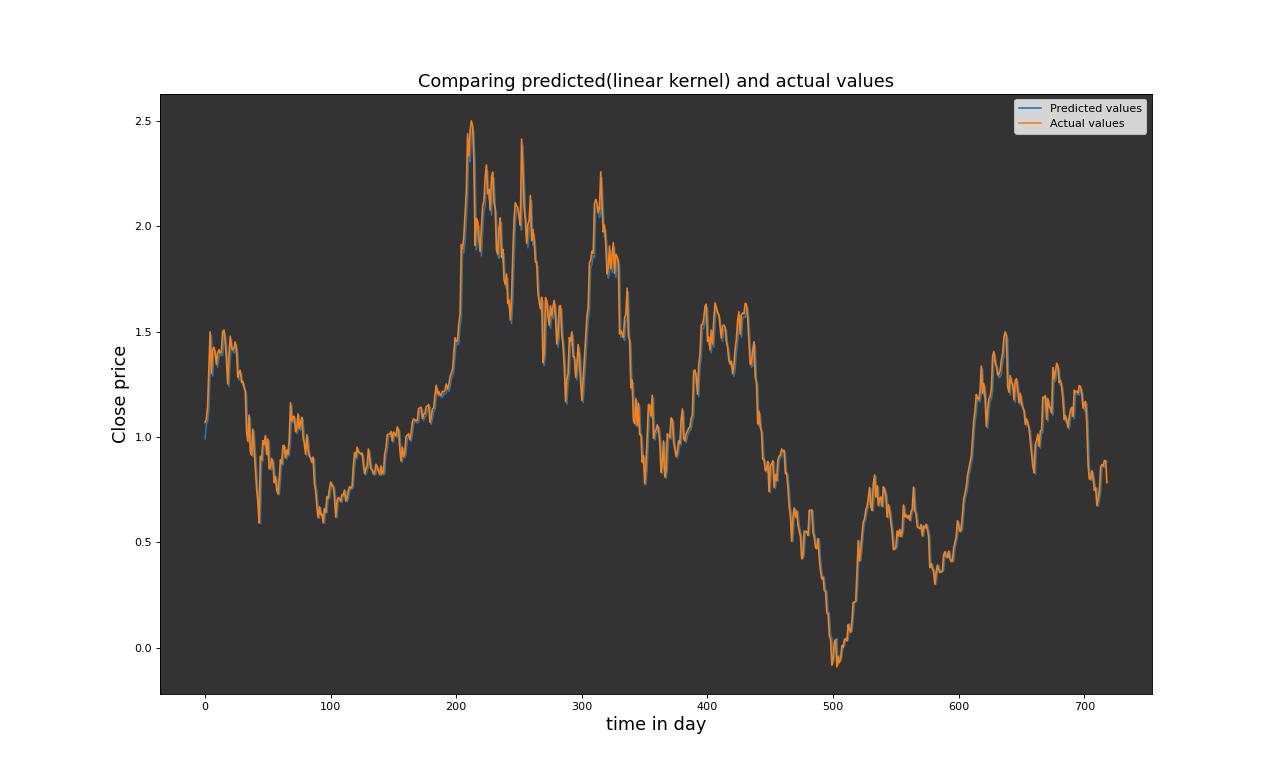
Linéaire (Linear) : Le noyau linéaire est le plus simple des noyaux SVM. Il s’agit essentiellement d’une fonction produit scalaire qui crée une frontière linéaire de séparation entre les classes dans l’espace des caractéristiques. Bien qu’il soit direct et efficace pour des ensembles de données linéairement séparables, il peut ne pas être aussi performant pour des données plus complexes.
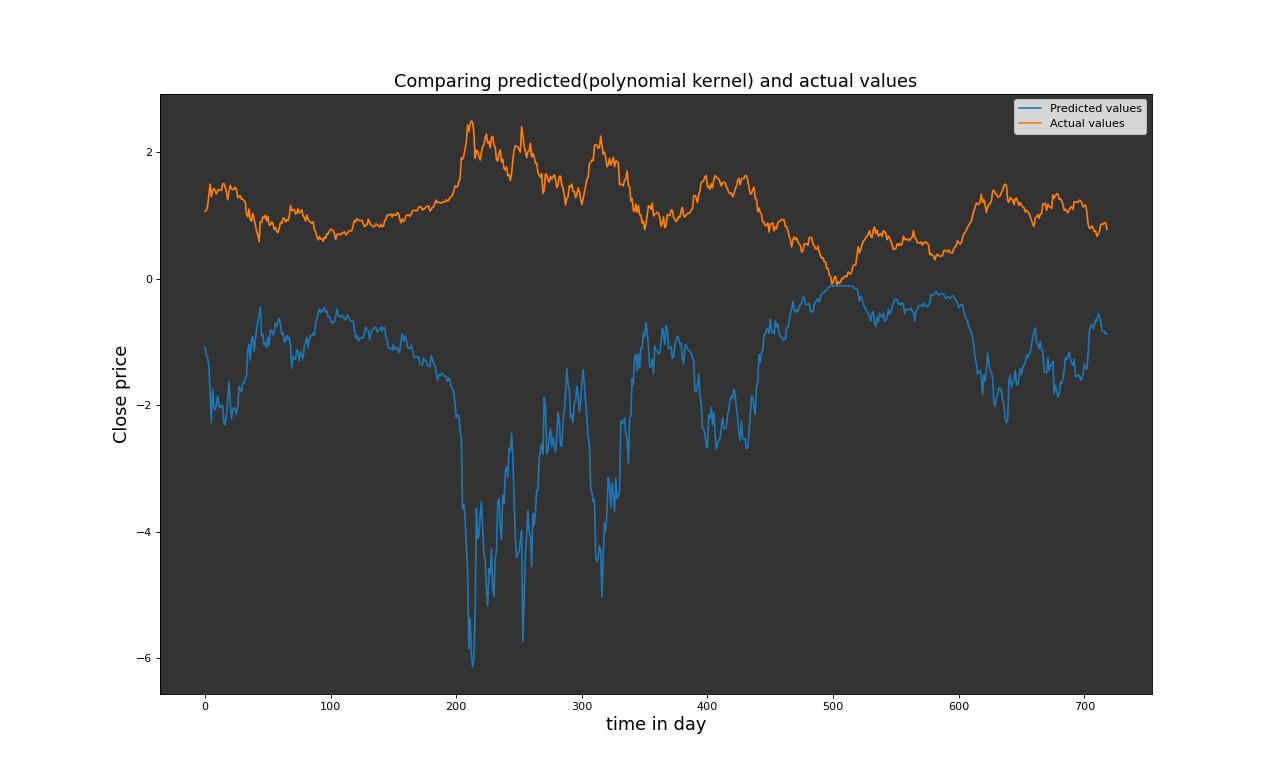
Polynomial : Le noyau polynomial est utilisé pour gérer des données qui ne sont pas linéairement séparables. Il permet de transformer l’espace des caractéristiques en introduisant des termes polynomiaux, ce qui permet de créer des frontières de décision non linéaires. Cependant, le choix du degré du polynôme peut affecter la performance, car une valeur trop élevée peut conduire à un surajustement.
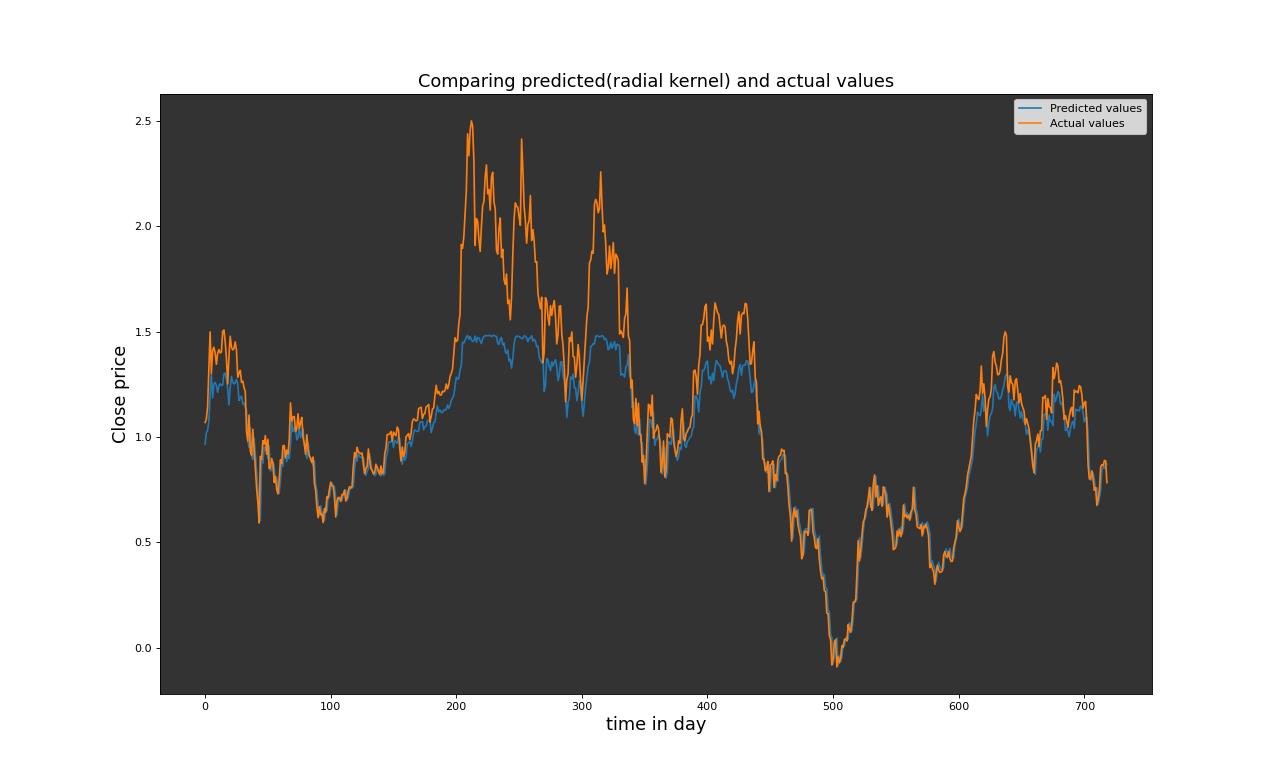
RBF (Radial Basis Function) : Le noyau RBF, ou gaussien, est l’un des noyaux les plus populaires en SVM. Il crée une frontière de décision non linéaire en transformant les données dans un espace de dimensions infinies. Il est particulièrement efficace pour des ensembles de données complexes et offre une grande flexibilité. Cependant, il nécessite le réglage de paramètres, tels que la largeur de la gaussienne, qui peut influencer la performance du modèle.

Data description

Tesla, Inc., une entreprise emblématique du secteur automobile, est sélectionnée pour l’analyse. Pour l’entraînement et le test des algorithmes et des modèles, nous avons choisi une période s’étendant de janvier 2013 à novembre 2023. Yahoo Finance fournit une base de données historique qui peut être utilisée pour l’entraînement du modèle de prédiction des cours de l’action de Tesla. Cette base de données historique propose des informations cruciales, comprenant les paramètres suivants :

▪ Date : La date à laquelle les valeurs suivantes ont été collectées.
▪ Open : La valeur d’ouverture de l’action de Tesla.
▪ High : La valeur la plus élevée atteinte par l’action de Tesla à cette date.
▪ Low : La valeur la plus basse atteinte par l’action de Tesla à cette date.
▪ Close : La valeur de clôture de l’action de Tesla pour cette date.
▪ Adj Close : La valeur de clôture de l’action de Tesla avant l’ouverture du marché le jour suivant, ajustée en tenant compte des actions corporatives et des distributions.
▪ Volume : Le nombre total d’actions de Tesla échangées pendant cette journée.

Ces données fourniront une base solide pour analyser les variations historiques des prix des actions de Tesla et faciliteront le développement et l’évaluation des modèles de prévision des cours de l’action pour la période spécifiée.

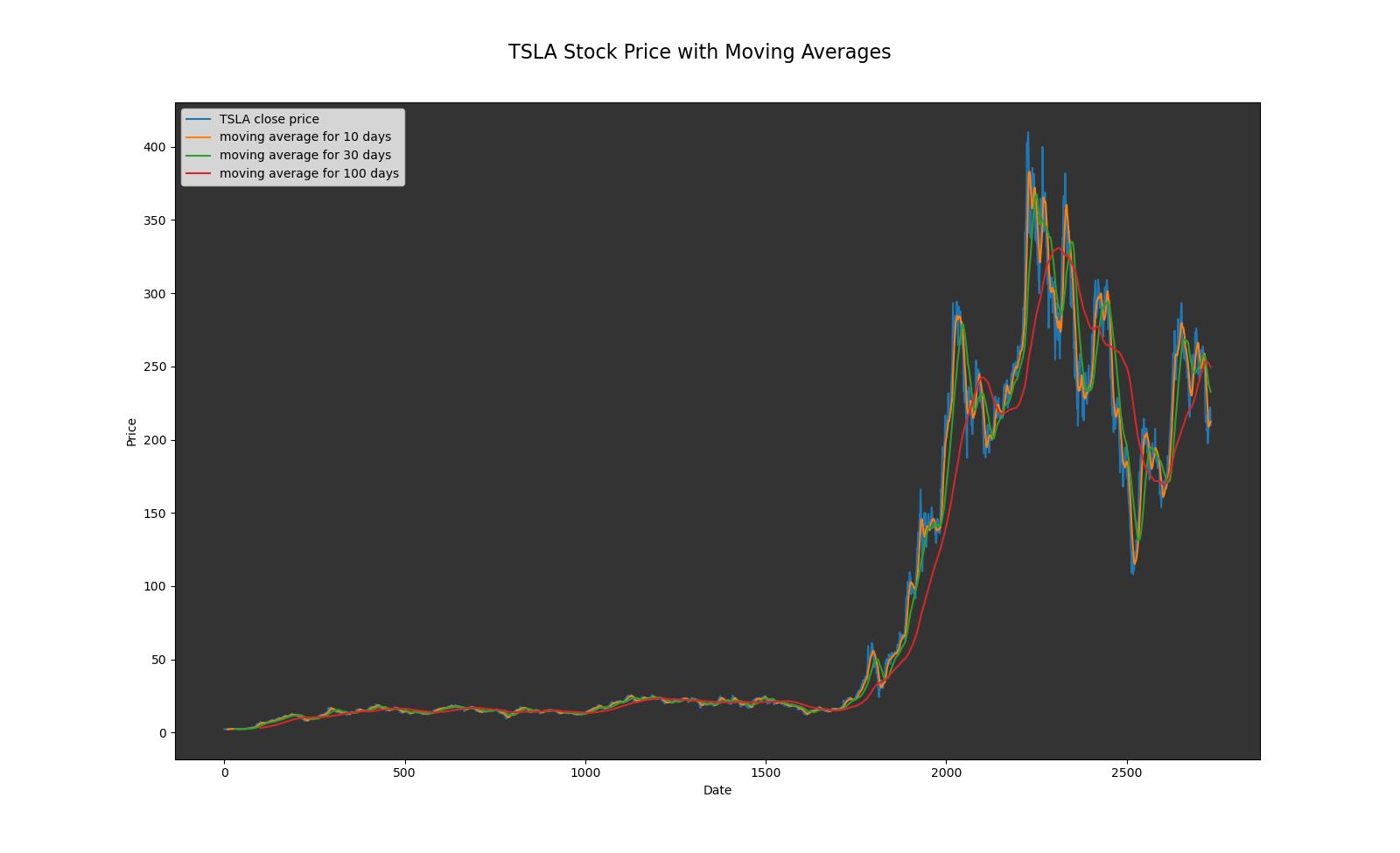
L’évolution de l’action de Tesla, Inc. de 2013 à aujourd’hui se caractérise par une tendance globale à la hausse, soutenue par des innovations technologiques et des lancements de nouveaux modèles. La période pré-2020 a été marquée par une croissance constante du cours de l’action, accompagnée d’une augmentation progressive du volume quotidien des échanges, soulignant l’intérêt croissant des investisseurs. Cependant, au début de 2020, la pandémie de COVID-19 a entraîné une chute significative des cours, illustrée par une baisse du volume des échanges. Malgré ces défis, Tesla a démontré une remarquable résilience, se rétablissant rapidement grâce à des facteurs tels que la reprise des activités, les développements technologiques et l’expansion continue de sa base de clients.

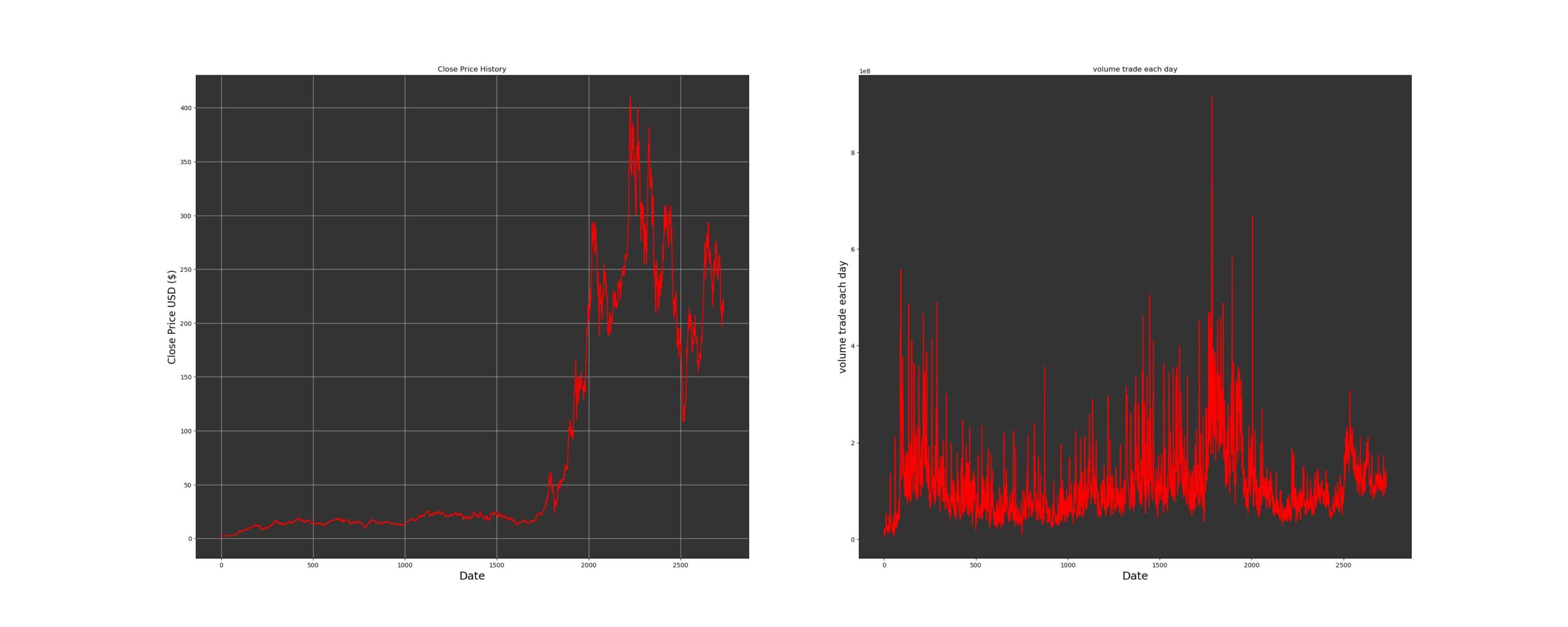
Les moyennes mobiles de 10, 30 et 100 jours offrent des perspectives clés sur la tendance à court, moyen et long terme du cours de l’action de Tesla. La moyenne mobile sur 10 jours, étant plus réactive aux fluctuations récentes, fournit une indication rapide des changements de direction du marché. La moyenne mobile sur 30 jours offre une perspective à moyen terme, lissant davantage les variations de prix et identifiant des tendances plus établies. Enfin, la moyenne mobile sur 100 jours, en tant que mesure à plus long terme, donne un aperçu de la tendance générale du marché sur une période significativement étendue, aidant à évaluer la stabilité et la durabilité des tendances. Ensemble, ces moyennes mobiles fournissent une analyse temporelle complète du comportement du cours de l’action de Tesla, aidant les investisseurs à mieux comprendre les dynamiques du marché à différentes échelles de temps.

Résumé

Selon la métrique R² et la RMSE, le modèle de machine à vecteurs de support avec un noyau linéaire s’est légèrement mieux ajusté en comparaison avec le modèle de machine à vecteurs de support utilisant la fonction de base radiale (RBF) et le noyau polynomial. Cependant, il est à noter que, pour nos données, le modèle RBF s’est ajusté beaucoup moins bien aux données. Dans l’ensemble, tous les modèles mentionnés ci-dessus, le SVM avec noyau linéaire affiche de meilleures performances. Cette observation peut être attribuée à la distribution aléatoire des données. En outre, il est important de souligner que les performances des modèles SVM, bien que linéaires semblent être plus adaptées à la nature de dispersion aléatoire des données. Ces résultats soulignent l’importance de choisir le bon type de noyau en fonction de la structure des données, montrant que le modèle linéaire SVM s’adapte mieux à la répartition aléatoire des données que les noyaux RBF et polynomial dans notre contexte d’analyse.