1. Introduction

Les données constituent la base de toute analyse statistique, sans elles aucune analyse factuelle ne peut être opéré. Même si leur collecte peut souvent sembler être évidente mais dans les faits cela n’est pas cas, car les données collectées peuvent parfois être fausse ou incomplète et une analyse statistique faites sur la base de données fausse ou incomplète est une analyse inconsistante. Pour cette raison, il est essentiel en amont d’une analyse statistique de bien traiter les données afin de palier à ces problèmes et ou manquements. Dans cet article, nous allons nous appesantir sur les données manquantes/incomplètes ainsi que leurs traitements.

Élément	Sexe	Âge	Éducation	Santé	Revenu net	…
1	Femme	40 – 45	Supérieur	Bien	?	…
2	Homme	30 – 35	Secondaire	Mauvaise	4500 – 5000	…
3	Femme	20 – 25	?	Moyen	4000 – 4500	…
4	Homme	20 – 25	Supérieur	?	?	…
5	Homme	30 – 35	Primaire	?	1500 – 2000	…
…	…	…	…	…	…	…

2. Causes des données manquantes

Les causes des données manquantes dans un échantillon peuvent être classées en trois grandes catégories, selon leur origine et leurs caractéristiques. Ces causes sont cruciales pour comprendre comment traiter ces données et minimiser leur impact sur l’analyse statistique. Parmi les causes liés aux données manquantes on distingue :

Les causes liées à la conception de l’étude
Questions mal formulées: Une question peu claire ou mal conçue peut entraîner un manque de réponse. Exemple : Une question trop complexe ou ambiguë décourage les réponses.
Erreurs techniques ou administratives: Des problèmes techniques (comme des erreurs dans le système de collecte de données) ou des oublis lors de la saisie des données peuvent conduire à des valeurs manquantes. Exemple : Une panne du système de sondage en ligne au moment de la collecte.
Split-Questionnaire-Design: Par conception, certaines questions sont posées uniquement à des sous-groupes de participants pour réduire la charge de réponse. Exemple : Une étude où des participants répondent à différentes versions d’un questionnaire.
Les causes liées aux individus ou particpants
Refus de répondre (Non-réponse): Les participants refusent de fournir certaines informations, souvent en raison de préoccupations liées à la vie privée ou à la sensibilité des questions. Exemple : Une personne ne souhaite pas révéler son revenu ou son âge.
Absence ou abandon (Unit-Nonresponse): Certains participants ne répondent pas du tout à l’enquête ou abandonnent avant la fin. Exemple : Dans une étude en ligne, certains répondants ferment le formulaire avant de le terminer.
Les causes liées aux évenements externs ou conditionsspécifiques
Problèmes liés à la mémoire ou à la connaissance: Les répondants peuvent ne pas se souvenir ou ne pas connaître la réponse à une question. Exemple : Une personne ne se souvient pas de la date exacte d’un événement passé.
Contexte environnemental ou social: Des facteurs tels que le stress, le manque de temps ou des événements inattendus peuvent empêcher les participants de répondre. Exemple : Une enquête menée pendant une catastrophe naturelle peut être incomplète.
Données perdues ou inaccessibles: Lors de la collecte ou du stockage, certaines données peuvent être perdues ou corrompues. Exemple : Des fichiers de données endommagés après une panne informatique.

3. Traitements des données manquantes

Dès lors qu’il a été constaté que l’enquête réalisée contient des données manquantes, il est impératif de traiter ce problème afin d’éviter d’obtenir des résultats faussés. Pour cela, il existe diverses méthodes de traitements des données manquantes.

a) La méthode naïve d’imputation

La méthode naïve d’imputation est un ensemble de techniques simples utilisées pour remplacer les valeurs manquantes dans un jeu de données. Ces méthodes ne prennent généralement pas en compte les incertitudes ou la structure complexe des données, ce qui peut introduire des biais ou sous-estimer la variabilité. Voici les principales méthodes naïves d’imputation :

L’imputation par la moyenne (mean imputation)

Elle consiste à remplacer les valeurs manquantes d’une variable par sa moyenne calculée à partir des observations disponibles. Elle a pour avantages d’être simple à implémenter mais par contre réduit la variabilité des données et peut biaiser les résultats.

L’imputation par la médiane (median imputation)

Elle consiste `remplacer les valeurs manquantes d’une variable par sa médiane. Son avantage réside dans le fait qu’elle est moins sensible aux valeurs extrêmes que la moyenne, par contre elle ne capture pas les relations entre variables.

L’imputation par la valeur la plus fréquente (mode imputation)

Cette méthode consiste à remplacer les valeurs manquantes par la modalité la plus fréquente. Elle est particulièrement utilisée pour les variables catégoriques. Comme avantage, cette méthode est facile à utiliser pour les données catégoriques par contre biaise la répartition des catégories.

L’imputation par régression simple

Elle utilise une relation linéaire entre les variables pour estimer les valeurs manquantes. Elles introduisent un lien avec les autres variables, par contre les valeurs imputées sont souvent trop précises et n’introduisent pas d’incertitude.

L’imputation par copie aléatoire (Hot Deck imputation)

Cette imputation consiste à remplacer une valeur manquante par une valeur observée similaire dans le jeu de données. Elle a pour avantage de maintenir la distribution des données. Comme inconvénients elle peut être arbitraire ou sensible aux choix des groupes similaires.

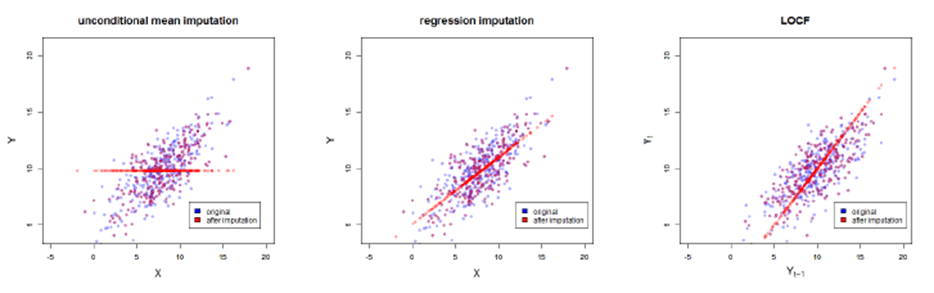
Fig. 1 : Aperçu des inconvénients des méthodes d’imputation naïves

Les méthodes sus cités sont certes faciles à implémenter mais elles introduisent plusieurs problèmes tels que la sous-estimation de la variabilité, l’introduction de biais et la non-représentation des relations complexes. Pour résoudre ces problèmes, il existe de méthodes modernes de traitements des données manquantes plus robuste et modernes.

Avant l’application des méthodes modernes de traitement des données manquantes, il est primordial tout d’abords d’identifier de quel type de mécanisme et de modèles de données manquantes nous avons à faire

b. Les mécanismes de données manquantes

Parmi les mécanismes existants, on distingue :

Les disparations complètement aléatoire (Missing completely at random : MCAR) : dans un MCAR la probabilité qu’une donnée soit manquante ne dépend ni des valeurs observées, ni des valeurs manquantes. En d’autres termes, les données manquent de manière complètement aléatoire. Dans ce mécanisme la probabilté qu’une valeur soit manquante est la même pour toutes les oberservations, quelles que soient leurs caractéristiques ou les valeurs des autres variables. Les valeurs manquantes n’introduisent pas de biais dans l’estimation des paramètres si l’analyse est effectuée uniquement sur les données disponibles.

Pour déterminer le mécanisme MCAR, on peut effectuer une analyse visuelle ou bien les test de Little, qui teste l’hypothèse nulle selon laquelle les données manquantes suivent un mécanisme MCAR.

Les disparution au hasard (Missing at random : MAR) : Les données sont dites MAR, lorsque la probabilité qu’une donnée soit manquantes dépennd uniquement des valeurs observées dans le jeu de données, mais pas des valeurs manquantes elles -mêmes. Ce mécanisme se caractérise par L’existence d’une relation avec les données observées. L’identification d’un MAR peut se faire à l’aide d’une analyse visuelle ou des modèles conditionnels (régression logistique etc.).
Les disparutions qui ne sont pas dûs au hasard (Not missing at random (NMAR) : Les données sont dites NMAR lorsqu’elles manquent en fonction des valeurs elles-mêmes qui sont manquantes. En d’autres termes, la probabilité qu’une donnée soit manquante dépend directement de la valeur de cette donnée manquante. Ce mécanisme est le plus complexe à traiter car il ne peut pas être expliqué par les variables observées ou des hypothèses simples. Ce mécanisme se caractérise par une dépendance intrinsèque, c’est-à-dire même avec avec des informations sur d’autres variables, l’absence des données ne peut pas être complètement expliquée.

c) Schéma des données manquantes

En plus de ces mécanismes, les données peuvent suivre différents modèles de valeurs manquantes :

Modèle univarié

Les valeurs manquantes apparaissent dans une seule variable / colonne.

Exemple : Un jeu de données où seule la colonne « âge » contient des valeurs manquantes.

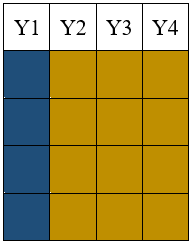
modèle multivarié (aléatoire/arbitraire)

Les valeurs manquantes sont réparties sur plusieurs variables sans schéma clair.

Exemple : Dans un questionnaire, différentes personnes omettent de répondre à différentes questions.

Modèle monotone

Les valeurs manquantes suivent un ordre particulier, souvent dans les études longitudinales.

Exemple : Dans une étude sur plusieurs années, certains participants abandonnent en cours de route, entraînant un manque de données pour les années suivantes.

Modèle monotone

Les valeurs manquantes suivent un ordre particulier, souvent dans les études longitudinales.

Exemple : Dans une étude sur plusieurs années, certains participants abandonnent en cours de route, entraînant un manque de données pour les années suivantes.

En résumé les données incomplètes apparaissent lorsque certaines valeurs manquent dans un ensemble de données. Ces données manquantes peuvent fausser l’analyse ou entraîner une perte d’informations. Il est donc essentiel de traiter avec soin les valeurs manquantes avant toute analyse.

d) Multiple imputation

L’imputation multiple est une méthode statistique permettant de remplacer les données manquantes dans des ensembles de données sans ignorer l’incertitude de ces estimations. Elle est principalement utilisée dans l’analyse de données, la recherche empirique et l’apprentissage automatique lorsque les données sont incomplètes.

Le principe de base de l‘imputation multiple est qu’au lieu d’estimer les valeurs manquantes une seule fois (comme dans le cas de l’imputation simple), l’imputation multiple consiste à répéter le processus d’imputation plusieurs fois (généralement entre 5 et 20 fois) afin de générer plusieurs valeurs plausibles. Cela présente deux avantages : maintien de l’incertitude naturelle concernant les valeurs manquantes et éviter les distorsions qui peuvent résulter d’une imputation simple.

Une imputation multiple se fait en 3 étapes :

Imputation : Plusieurs (par exemple 5) ensembles de données complets sont générés en estimant les valeurs manquantes de différentes manières (généralement à l’aide des modèles tels que MCMC, de modèles de régression ou de Predictive Mean Matching).

Analyse : Chacun de ces ensembles de données complets est analysé individuellement (par exemple par régression, comparaison des moyennes, etc.).

Regroupement : Les résultats des analyses individuelles sont regroupés selon des règles spécifiques (par exemple, les règles de Rubin) – les variances sont également combinées afin de tenir compte de l’incertitude.

La méthode d’imputation multiple part du principe que les données sont manquantes de manière aléatoire (MAR), c’est-à-dire que l’absence de valeurs dépend des données observées et non des données manquantes. L’imputation multiple peut être réaliser sur R à l’aide des paquets tel que mice, Amelia et missForest et sur python à l’aide de fancyimpute et sklearn.impute.IterativeImputer.

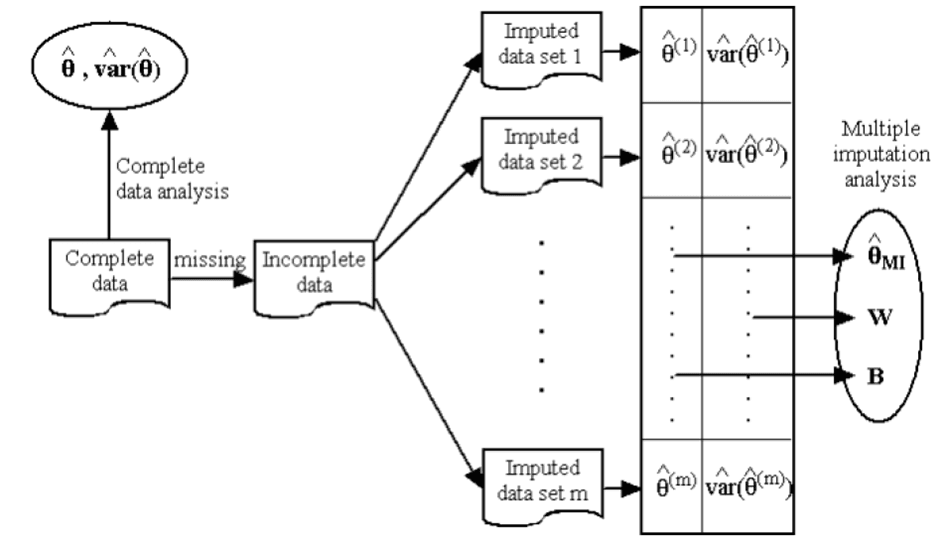
Fig.2 : principe de la multiple imputation

e) Imputation bayésienne

L’imputation bayésienne est une approche du traitement des données manquantes basée sur les statistiques bayésiennes. Les valeurs manquantes ne sont pas simplement remplacées par des estimations fixes, mais considérées comme des variables aléatoires avec des distributions de probabilité. L’objectif est d’obtenir des estimations plus réalistes et une quantification correcte de l’incertitude.

Le principe de base de l’imputation bayésienne est qu’au lieu d’utiliser une valeur ponctuelle (par exemple la moyenne), le théorème de Bayes permet de calculer une distribution a posteriori des valeurs manquantes, sur la base :

des données observées,
d’un modèle supposé (par exemple une distribution normale),
et d’une distribution a priori pour les valeurs inconnues.

Ensuite, plusieurs valeurs plausibles (échantillons) sont extraites de cette distribution afin d’imputer les valeurs manquantes. La Procédure d’imputation se déroule en 5 étapes qui sont :

Définir le modèle : définissez une distribution de probabilité pour les données (par exemple, une distribution normale pour les données métriques).
Définir la distribution a priori : choisissez une distribution qui exprime l’incertitude sur les paramètres (par exemple, une distribution normale avec une moyenne et une variance inconnues).
Calculer la distribution a posteriori : à l’aide des données observées, calculez la distribution conditionnelle des valeurs manquantes.
Imputation par tirage à partir de la distribution a posteriori : générez plusieurs ensembles de données « complets » en tirant au hasard des valeurs de cette distribution.
Analyse et regroupement : chaque ensemble de données complet est analysé séparément, puis les résultats sont combinés (comme dans le cas de l’imputation multiple).

Les avantages d’une imputation bayésienne sont : une représentation réaliste de l’incertitude, une intégration des connaissances préalables possible fondé sur des statistiques, en particulier pour les petits échantillons

Les inconvénients d’une imputation bayésienne sont : les calculs sont complexes (simulation, MCMC nécessaire), la mise en œuvre est également complexe et nécessite des connaissances statistiques

Les outils tel que R avec les paquets comme mice, Amelia, rjags, brms et BayesMI et python avec les paquets comme PyMC, scikit.mice, statsmodels permettent la mise en œuvre d’une imputation bayésienne.

Annexe

Ci-joint queleques lignes de code pour analyser les valeurs manquantes.

library(VIM)

library(mice)

aburl = ‘http://archive.ics.uci.edu/ml/machine-learning-databases/abalone/abalone.data’

abnames = c(‘sex’,’length’,’diameter’,’height’,’weight.w’,’weight.s’,’weight.v’,’weight.sh’,’rings’)

abalone = read.table(aburl, header = F , sep = ‘,’, col.names = abnames)

attach(abalone)

View(abalone)

# We perform a linear regression to see which variable has a significant influence on rings.

lin.mod1 <- lm(rings~.,data=abalone)

summary(lin.mod1)

detach(abalone)

# The variables length and sex have no significant influence on rings.

# We remove the variables length and sex from our model.

abalone <- abalone[,-c(1,2)]

abalone$rings <- as.numeric(abalone$rings)

str(abalone)

# Regression Model

lin.mod2 <- lm(rings~ .,data = abalone)

summary(lin.mod2)

# all Variable are now significant

# Sample

n <- 1000

data <- sample(nrow(abalone),n)

p.mis <- 0.3

# 30% from rings are MCAR

set.seed(1234)

abalone.mcar <- abalone

mis.mcar <- sample(n,n*p.mis,replace = FALSE)

abalone.mcar$rings[mis.mcar] <- NA

summary(abalone.mcar$rings)

# 30% from rings are MAR

abalone.mar <- abalone

mis.mard <- qnorm(0.3,mean(abalone.mar$rings),sd(abalone.mar$rings))

q.rings <- quantile(abalone.mar$rings,0.3)

mis.mard <- abalone.mar$rings < q.rings # erzeugt logical vektor

abalone.mar$rings[mis.mard] <- NA

summary(abalone.mar$rings)

# Model missingnes via linear regression model

Mmis.mar.p <- 2.8 + 11.6*diameter + 11.7*height + 9.2*weight.w -20.2*weight.s -9.9*weight.v + weight.sh + rnorm(n,0,3)

detach(abalone.mar)

plot(density(Mmis.mar.p))

abline(v=quantile(Mmis.mar.p,p.mis), col = « red »)

mis_data_MAR <- quantile(Mmis.mar.p,p.mis)

mean(as.numeric(mis_data_MAR))

## Visualization von Missing Data

# for MCAR

aggr(abalone.mcar) # Blockwise missing data pattern

barMiss(abalone.mcar) # oder

marginplot(abalone.mcar[,-c(2,3,4,5,6)])

# for MAR

aggr(abalone.mar) # Blockwise missing data Pattern.

barMiss(abalone.mar)

marginplot(abalone.mar[,-c(2,3,4,5,6)])

# We are now performing three different simulations

# (mean, imputation, regression imputation, norm imputation and Pmm imputation)

# and comparing their bias, coverage and variance.

set.seed(1234)

R <- 1000 # Number of Imputation

M <- 10 # Number of Imputation

runs <- 1 # Number of iterations

## Model based imputation method

## with MCAR

## mean Imputation

# mean before deletion

mean.est <- mean(abalone$rings)

ci <- t.test(abalone$rings)$conf.int

ci_low <- ci[1]

ci_upp <- ci[2]

var(abalone$rings)

# mean after imputation

RS.imp <- matrix(nrow = R,ncol = 3)

# functions for diagnostics

coverage <- function(value, CI.low, CI.upper){

ifelse(CI.low <= value && CI.upper >= value,1,0)

}

bias <- function(value,mean.est) {

bias <- (mean.est-value)

return(bias)

}

Varz <- function(value) {

Varz <- var(value)

return(Varz)

}

for (i in 1:1000) {

mis.mcar <- sample(n,n*p.mis,replace = FALSE)

abalone.mcar$rings[mis.mcar] <- NA

mean.est.imp <- mean(abalone.mcar$rings,na.rm = TRUE)

abalone.mcar$rings[is.na(abalone.mcar$rings)] <- mean.est.imp

RS.imp[i,] <- c(coverage(mean.est.imp,ci_low,ci_upp),bias(mean.est.imp,mean.est),Varz(abalone.mcar$rings))

}

RS.imp[1,]

# Comparison

mean.est

var(abalone$rings)

mean.est.imp

Varz(abalone.mcar$rings)